 : 3D Ball Trajectory Estimation From 2D Monocular Tracking
: 3D Ball Trajectory Estimation From 2D Monocular Tracking
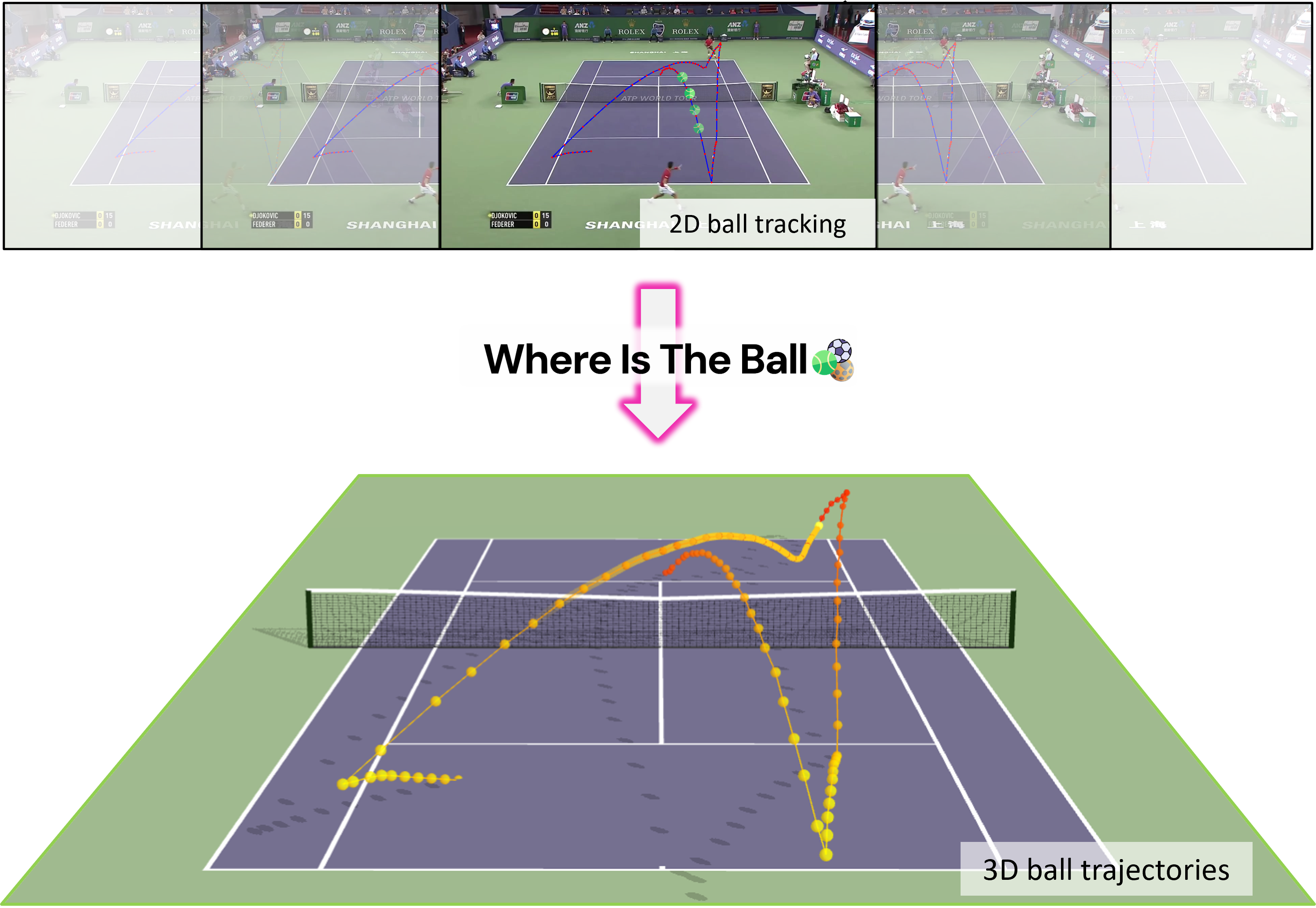




* Simulation was created using the Unity engine. Unity is not affiliated with or endorsing this project.
We present a method for 3D ball trajectory estimation from a 2D tracking sequence. To overcome the ambiguity in 3D from 2D estimation, we design an LSTM-based pipeline that utilizes a novel canonical 3D representation that is independent of the camera's location to handle arbitrary views and a series of intermediate representations that encourage crucial invariance and reprojection consistency. We evaluated our method on four synthetic and three real datasets and conducted extensive ablation studies on our design choices. Despite training solely on simulated data, our method achieves state-of-the-art performance and can generalize to real-world scenarios with multiple trajectories, opening up a range of applications in sport analysis and virtual replay.
Our goal is to recover the 3D trajectory of a ball from a sequence of 2D tracked positions. One naive approach is to directly regress 3D coordinates from the 2D tracking pixels. However, this method does not ensure reprojection consistency with the original 2D inputs. Additionally, using 2D tracking pixels as input implicitly ties the model to camera parameters (e.g., focal length, position, and orientation), which limits generalization across different viewpoints. To overcome these limitations, we transform each 2D input into a plane-point representation that removes dependency on the camera setup, enabling training on multiple cameras and inference within a single network. Rather than predicting full 3D coordinates, we estimate the ball’s height over time to maintain reprojection consistency with the original 2D observations. We also introduce a relative-absolute input encoding, which improves generalization to spatial shifts and helps the model achieve location equivariance.
Our pipeline consists of three main LSTM-based components: 1) the End-of-Trajectory (EoT) Network, which predicts whether the ball is ending its current motion or changing direction (e.g., after a player’s hit); 2) the Height Network, which estimates the ball’s height over time and is later used to reconstruct the full 3D trajectory; and 3) the Refinement Network, which further adjusts the predicted 3D coordinates for improved accuracy and smoothness.
Explore the results of our method in an interactive visualizer. You can view the 3D trajectories and ground truth data for each test scenario.
Note: Best viewed in a desktop browser.
 TrackNet (Tennis) - Synthetic
TrackNet (Tennis) - Synthetic

 TrackNet (Tennis) - Real
TrackNet (Tennis) - Real

 MoCap – Synthetic
MoCap – Synthetic

 MoCap – Real
MoCap – Real

 IPL (Soccer) - Synthetic
IPL (Soccer) - Synthetic

 IPL (Soccer) - Real
IPL (Soccer) - Real

 Comparison to SOTA – Synthetic Single-Launch Trajectory
Comparison to SOTA – Synthetic Single-Launch Trajectory

@inproceedings{ponglertnapakorn2025ball,
title={Where Is The Ball: 3D Ball Trajectory Estimation From 2D Monocular Tracking},
author={Ponglertnapakorn, Puntawat and Suwajanakorn, Supasorn},
booktitle={Proceedings of the Computer Vision and Pattern Recognition Conference},
pages={6122--6131},
year={2025}
}